Beta 分布
[[概率密度函数]] #card
$\operatorname{Beta}(\mu \mid a, b)=\frac{\Gamma(a+b)}{\Gamma(a) \Gamma(b)} \mu^{a-1}(1-\mu)^{b-1}$
$\Gamma$ 是 [[gamma函数]]
期望 #card
$\mathbb{E}[\mu]=\frac{a}{a+b}$
方差 #card$\operatorname{var}[\mu]=\frac{a b}{(a+b)^2(a+b+1)}$
和 [[二项分布]] 的区别 #card二项分布对成功次数 x 进行建模
beta 分布对成功概率 p 进行建模

- a 和 b 对分布图像的影响 #card
随着 $\alpha$ 的增加(成功事件增多),概率分布的大部分将向右移动。
另一方面,$\beta$ 的增加会使分布向左移动(更多失败事件)。
同样,如果我们同时确定 $\alpha$ 和 $\beta$ 都增加,则分布将变窄。
例子 [[@PRML Note 前十一章]] 2-006
ls-type:: annotation
hl-page:: 62
hl-color:: purple
以及 ((654bb13c-db71-49d4-ad0e-123ec812c258))
[[二项分布]] 概率函数
- $p(m \mid N, \mu)=C_N^m \mu^m(1-\mu)^{N-m}$
结合 Beta 先验分布,根据[[贝叶斯公式]]后验分布有
$\begin{aligned} p(\mu \mid m, N, a, b) & \propto p(m \mid N, \mu) p(\mu \mid a, b) \ & =C_N^m \mu^m(1-\mu)^{N-m} \frac{\Gamma(a+b)}{\Gamma(a) \Gamma(b)} \mu^{a-1}(1-\mu)^{b-1} \ & \propto \mu^{m+a-1}(1-\mu)^{N-m+b-1}\end{aligned}$
n 和 m 都是已知
超参数 a 和 b 是先验中时间发生的次数和不发生的次数,a+b就是有效观察次数
根据这个公式可以看出先验对后验的影响
根据 $p(\mu \mid m, l, a, b)=\frac{\Gamma(m+a+l+b)}{\Gamma(m+a) \Gamma(l+b)} \mu^{m+a-1}(1-\mu)^{l+b-1}$ 后验分布也服从 Beta 分布
- 根据 $\mathbb{E}[\mu]=\frac{a}{a+b}$
得到事件发生的概率期望等于事件发生次数除以总次数
+ 二项分布中 $p(x=1 \mid D)$ 预测的分布就是 $\mathrm{E}[\mu \mid D]$
+ $p(x=1 \mid D)=\mathrm{E}[\mu \mid D]=\frac{m+a}{N+a+b}=\frac{m+a}{m+a+l+b}$
+ l = N-m,后验中时间不发生的次数
+ 次数增加,m 和 N 值会变大,当趋于无穷时,a 和 b 可以忽略。
+ 试验次数少,受先验影响大,反之相反。
+ 试验次数多到一定程度后,先验几乎没有影响,后验估计和极大似然估计趋于一致。
2-008
ls-type:: annotation
hl-page:: 63
hl-color:: purple
[[Bayesian Online Learning]] ((654e45e1-d673-4eeb-806f-9334ee4ee3d9))- a+b 值越大,u 取值越集中。根据 $\operatorname{var}[\mu]=\frac{a b}{(a+b)^2(a+b+1)}$
a和趋于无穷时,u 的方差趋于 0。对应试验次数越多,u 的取值越集中,不确定(方差)越小。#card
+ 下图是 beta 分布概率密度曲线
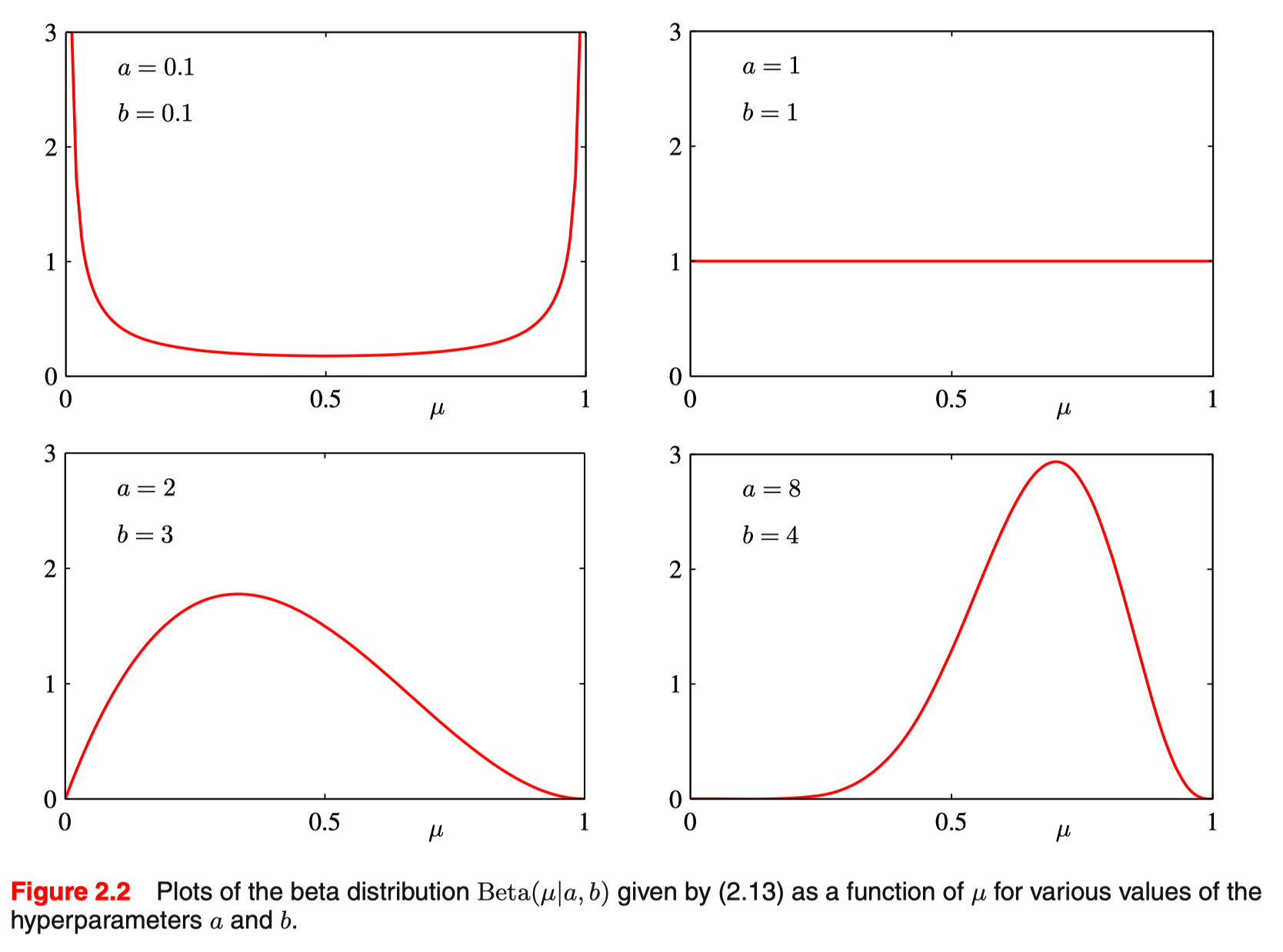
+ #card [\[\[试验次数和后验分布的关系\]\]](/post/logseq/%E8%AF%95%E9%AA%8C%E6%AC%A1%E6%95%B0%E5%92%8C%E5%90%8E%E9%AA%8C%E5%88%86%E5%B8%83%E7%9A%84%E5%85%B3%E7%B3%BB.html) 随着试验次数的增加(数据集的变大),未知参数的取值越来越集中?
ls-type:: annotation
hl-page:: 63
hl-color:: yellow
+ 随着试验次数的增加,后验分布的不确定性会越来越小?
ls-type:: annotation
hl-page:: 63
hl-color:: yellow
+ 答案是:在一般情况下,理论上的确有这样的趋势,但对于某些特定的数据集则不一定。
ls-type:: annotation
hl-page:: 63
hl-color:: yellow
[[@例子:概率的概率]]
[[不同 beta 分布形状]]